the four color problem

Another post fueled by interest in all things geeky. Hell. It's math this time. And it's about something called the four color theorem. A seemingly simple theorem, with certain ... er ... beauties, that caught my eye, and thus led to me writing this post.

/*sheepish grin
the angle brackets are better off for expressing feelings but Blogger's smart arse word processor very inconveniently considers any starting angle bracket to be the beginning of an html tag and all oddities arise. Hence the C/C++ style comments. Lol. */

The Four Color Theorem in its bare bones states that, (erm ... quoting Wikipedia) given any separation of a plane into contiguous regions, producing a figure called a map, no more than four colors are required to color the regions of the map so that no two adjacent regions have the same color. Point to note : two regions meeting at points can have the same color


Well, I am myself not the absolute authority in the four color theorem, and any such assumptions gathered, or unintentionally implied should be ... discarded immediately. Ahem.

The beauty I referred to in the opening paragraph is the method used to deal with these map coloring problems.

/*I know how suicidal the American spellings look, but unfortunately none of the browsers I use have spell check for any form English on this side of the Atlantic, so ...*/

Yes, so coming back to the method. Here's how it goes.

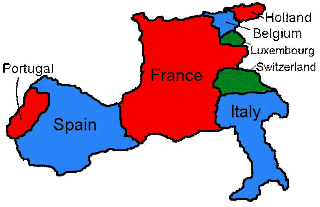
Consider the following map, showing a few countries of West Europe.

/* Pics taken from http://www.ctl.ua.edu/math103/mapcolor/mapcolor.htm, but as you can check, I've tried to explain in my own words */

The goal is too color the map such that no two countries sharing a common border have the same color. (Also, as a side information the minimum number of colors needed to colour a map is called the chromatic number of the map.) The completed map should look something like this.

So how to go about the predicament? Here's how.

1. We replace each country with circles, maintaining a roughly correct relative orientation. 
2. Whenever two countries share a common border, we join the two corresponding circles with a straight line.
3. We ensure that multiple common borders are taken care of ... France's with Belgium, Luxembourg, Switzerland and Italy.
4. Now color the circles such that a) two circles at the end of each line segment have different colours and b) the least number of colors are used.

the steps in pictures :

Done :-) Well that's about it. If it seems a bit too abrupt, my apologies. :-)